참고 문헌 출처: https://wikidocs.net/33520 , https://wikidocs.net/184216 ,
갑자기 전문성이 없는 내 자신에 대한 깊은 허탈감과 회의감을 느껴 조금은 공부한 척 해보려고 한다.
일단 파인튜닝이란 쉽게 생각하면 딥러닝 모델을 만든다고 했을 때 A라는 주제에 대해서 학습시킨다면 A에 대해서 잘 알게 된다. 근데 시간적 또는 효율적 비용적인 이유에서 A에 대해서 학습시킨 가중치를 가지고 B에 대해서 학습시키게 되면 A 도 알고 B도 아는 제너럴리스트 LLM을 만들 수 있다. 이것을 전이학습이라고 하는데 주로 모델의 후반부에 있는 분류기(Classifier) 레이어만 교체하고, 기존의 특징 추출기 부분은 그대로 동결(freeze)한 채 새로운 데이터에 맞춰 새로운 분류기만 학습시키는 방식을 주로 사용한다.
그래서 파인 튜닝이란 전이 학습의 한 방법으로, 사전 훈련된 모델의 전체 또는 일부 레이어를 새로운 데이터셋에 맞게 재학습(retaining)시키는 과정이다. 기존 모델의 가중치를 미세하게 조정하여 새로운 작업에 더 정밀하게 최적화 시키는 것을 목표로 하는 것이다.
특히, 기존의 모델과 새로운 작업 간의 도메인(분야) 차이가 크거나, 충분한 양의 새로운 데이터가 있을 때 효과적이다. 학습률을 낮게 설정하여 기존에 학습된 지식이 급격히 손상되지 않게 하는 것이 중요하다.
쉽게 생각하면 “구글이 gemma3를 만들때는 전이학습을 사용했고 오픈소스로 배포된 gemma3를 다운 받아서 커스텀 하고 싶은 양반들은 gemma3를 파인 튜닝했다는 소리”라는 의미이다.
구글은 방대한 데이터셋을 가지고 있다. 따라서 전이학습이 걔네들한테나 쉽다는 의미이고 일반인들은 한정된 데이터셋을 가지고 시작해야 하므로 거의 파인튜닝 외에는 선택지가 남지 않는다.
이런식으로 가다 보면 RAG를 쓰는 이유도 알게 되는데 매번 갱신되는 지식에 대해서 매번 파인 튜닝을 할 수는 없으니 RAG를 통해 외부 데이터에 대해 더욱 유연하게 대응하려는 목적이 있는 것이다.
우선 내가 아는 내용을 떠들어 대려고 한다.
우선 토크나이저의 하는 일과 워드 임베딩에 대해서이다.
우선 우리가 “Cat is cute”라는 문장을 가지고 생각해보자.
토크나이저: 텍스트를 숫자로
- 텍스트 분할 ‘Cat is cute’ -> [‘Cat’ , ‘is’ , ‘cute’]로 쪼갠다.
- 어휘사전 매핑: 각 토큰을 고유 ID로 변환. 예) 어휘 사전 = {“cat”: 5, “is” : 12 , “cute” 45} -> [5, 12, 45]
- 추가 처리: 패딩, 트렁케이션, 특수 토큰([CLS], [SEP])추가. [CLS, cat, is , cute, SEP] -> [101, 5, 12, 45, 102].
워드 임베딩: ID를 벡터로
역할: 토큰 ID를 고차원 밀집 벡터로 변환. 이 벡터는 단어의 의미를 포착
비유: 도서관 책 번호(5번)를 받아 책의 내용을 요약한 “정보 카드” ([0.4, 0.1, -0.3, ….])으로 바꾸는 과정. 이카드는 책(단어)의 의미를 숫자로 압축
우선 이 임베딩 방식에 대해서 ‘원 핫 인코딩’으로 하면 되지 않겠느냐라는 생각에 대해서 원핫인코딩은 단어의 개수가 늘어나면 벡터의 차원이 한 없이 커진다는 단점이 존재한다. 원-핫 벡터로 표현할 때는 갖고 있는 단어사전에 10000단어의 단어가 존재하면 원핫벡터는 10000차원이 되어 매우 비효율적이다.
이는 매우 큰 공간적 낭비이다. 이러한 것을 희소 표현(sparse Representation)이라고 한다.
이러한 희소표현과 반대되는 표현으로는 밀집 표현(Dense Representation)이 있다.
밀집 표현은 벡터의 차원을 단어 집합의 크기로 상정하지 않는다. 사용자가 설정한 값으로 모든 단어의 벡터 표현의 차원을 맞춘다. 또한, 이 과정에서 더 이상 0과 1만 가진 값이 아니라 실수값을 가지게 된다.
EX) 강아지 = [ 0 0 0 0 1 0 0 0 0 0 0 0 … 중략 … 0] # 이때 1 뒤의 0의 수는 9995개. 차원은 10000
이것은 희소 표현으로 강아지를 표현한 것이다.
이것을 밀집 표현의 차원을 128로 설정하고 표현하면 , 모든 단어의 벡터 표현의 차원은 128로 바뀌면서 모든 값이 실수가 된다.
강아지 = [0.2, 1.8, 1.1, -2.1, 1.1, 2.8 … 중략 …] #이 벡터의 차원은 128
이 경우 벡터의 차원이 조밀해졌다고 해서 밀집 벡터(dense vector)라고 함.
이러한 dense vector를 만드는 방법 중에는 word2vec이란 방법이 있다.
Word2Vec은 “비슷한 문맥에서 등장하는 단어는 비슷한 의미를 가진다”는 분포 가설(Distributional Hypothesis)을 기반으로 작동함.
- 희소 표현(Sparse Representation): 앞서 원-핫 인코딩을 통해서 얻은 원-핫 벡터는 표현하고자 하는 단어의 인덱스의 값만 1이고 나머지는 전부 0으로 표현되는 벡터 표현 방법이었는데, 이러한 희소 표현은 각 단어 벡터간 유의미한 유사성을 표현할 수 없다는 단점이 있었고, 대안으로 단어의 의미를 다차원 공간에 벡터화하는 방법을 사용하는데 이러한 표현을 분산 표현(distributed representation)이라고 함. 이러한 분산 표현을 이용하여 단어 간 의미적 유사성을 벡터화 하는 작업을 워드 임베딩(embedding)이라 부르며, 이렇게 표현된 벡터를 임베딩 벡터(embedding vector)라고 함.
- 이렇게 분포 가설을 기반으로 ‘비슷한 문맥에서 등장하는 단어들은 비슷한 의미를 가진다’라는 가정하에 만들어 진다. 그리고 Word2Vec을 사용하여 저차원에 단어의 의미를 여러 차원에다 분산하여 표현하면, 단어 벡터 간 유의미한 유사도를 계산 할 수 있다. 이를 위한 대표적인 학습 방법이 Word2Vec이다.
이 Word2Vec에는 두 가지 주요 아키텍쳐가 있다.
CBOW:
- 입력: 주변 단어(문맥 단어)의 벡터
- 출력: 중심 단어(타겟 단어)의 벡터
- 예: “The cat is very cute” 에서 [“The” , “is” , “very” , “cute”]를 입력으로 받아 “cat”을 예측.
- 특징: 문맥 단어를 평균화해 타겟 단어를 예측, 계산이 빠르고, 빈번한 단어에 적합.
즉, 주변에 있는 단어들을 입력으로 중간에 있는 단어들을 예측하는 방법이다.
Skip-gram
- 입력: 중심 단어의 벡터
- 출력: 주변 단어(문맥 단어)의 벡터.
- 예: “cat”을 입력으로 받아 [“The” , “is” , “very” , “cute”]를 예측
- 특징: 희귀 단어에 더 효과적이며, 더 많은 문맥 정보를 학습. 현대적으로 더 많이 사용됨.
즉, 중심 단어에서 주변 단어를 예측하는 방법이다.
CBOW에 대해서 더 자세히 알아보자.
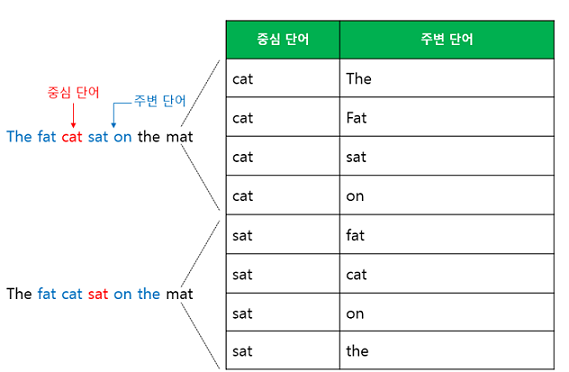
“The fat cat sat on the mat”
예를 들어서 갖고 있는 코퍼스에 위와 같은 예문이 있다고 해보자.
[‘The’ , ‘fat’ , ‘cat’, ‘on’, ‘the’ , ‘mat’]으로부터 sat을 예측하는 것은 CBOW가 하는 일이다.
이때 예측해야할 단어를 ‘sat’ 으로 하는 것이다.
그렇다. CBOW는 마치 여러 증거(주변 단어)를 모아 범인(중심 단어)가 누구인지 추리하는 것과 유사하다. 이미 존재하는 단서들을 바탕으로 하나의 결론을 도출하는 수렴적 사고에 가깝다.
skip-gram방식은 하나의 중심단어를 보고 주변에 어떤 단어들이 올지 예측하는데
이는 마치 하나의 사건을 통해 발생 가능한 여러 상황을 상상하는 것과 유사하다. 하나의 사실로부터 여러 가능성을 펼쳐가는 발산적 사고에 가깝다.
일단 용어는
중심단어 -> center word,
주변단어 -> context word
중심단어를 예측하기 위해서 앞, 뒤로 몇 개의 단어를 볼지를 결정해야 하는데 이 범위를 윈도우(window)라고 한다. 예를 들어 윈도우 크기가 2이고, 예측하고자 하는 중심 단어가 sat이라고 한다면 앞의 두 단어인 fat과 cat, 그리고 뒤의 두 단어인 on, the를 입력으로 사용한다.
윈도우의 크기가 n이라고 한다면, 실제 중심 단어를 예측하기 위해 참고하려고 하는 주변 단어의 개수는 2n이다.
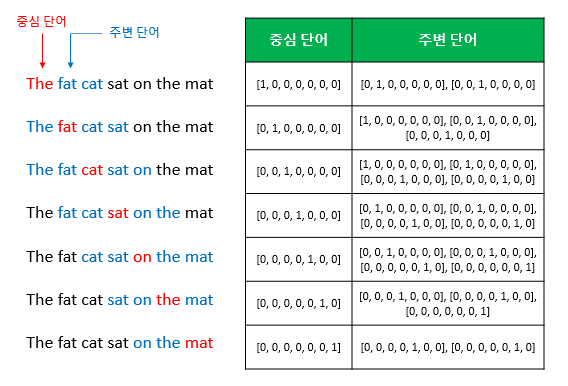
윈도우 크기가 정해지면 윈도우를 옆으로 움직여서 주변 단어의 선택을 변경해가며 학습을 위한 데이터 셋을 만드는데 이 방법을 슬라이딩 윈도우(sliding window)라고 한다.
위 그림의 우측그림은 중심 단어와 주변 단어를 어떻게 선택했을 때에 따라서 각각 어떤 원-핫 벡터가 되는지를 보여 준다.
윈도우의 크기가 2일 때, 슬라이딩 윈도우가 어떤 식으로 움직이면서 데이터 셋을 만드는 지 보여준다.
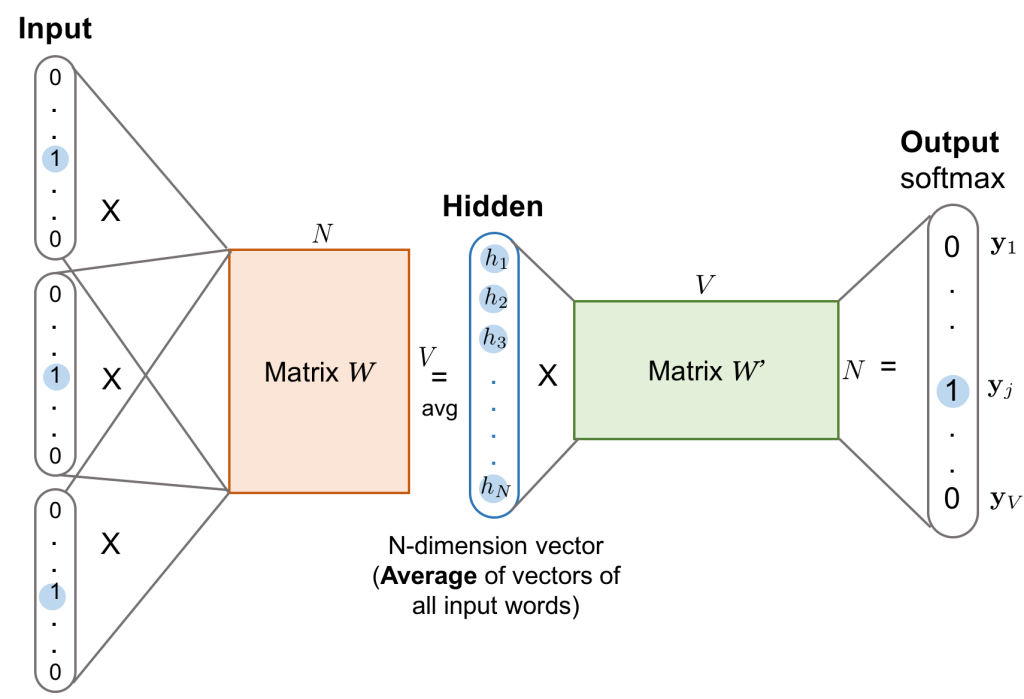
위 그림은 CBOW 신경망의 구조이다. 주변 단어들을 Avg 하는 부분이 보인다.
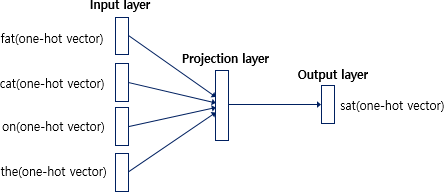
CBOW 신경망을 간단히 도식화 한 그림이라고 한다.
입력층(Input Layer)의 입력으로서 앞, 뒤로 사용자가 정한 윈도우 크기 범위 안에 있는 주변 단어들의 원-핫 벡터가 들어가게 되고, 출력층(Output layer)에서 예측하고자 하는 중간 단어의 원-핫 벡터가 레이블로 필요하다.
위 그림에서 알 수 있는 사실은 Word2Vec은 은닉층이 다수인 딥 러닝 모델이 아니라 은닉층이 1개인 얕은 신경망(shallow neural network)라는 점이다. 또한 Word2Vec의 은닉층은 일반적인 은닉층과 갈리 활성화 함수가 존재하지 않으며, 룩업 테이블이라는 연산을 담당하는 투사층(projection layer)이라고 부르기도 함.
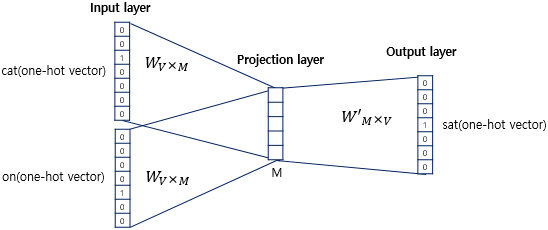
동작 메커니즘에 대해서 더 상세하게 알아보자.
위 그림에서 주목해야 할 점은 두 가지인데, 하나는 투사층의 크기가 M이라는 것이다.
CBOW에서 투사층의 크기 M은 임베딩 하고 난 벡터의 차원이 된다.
위의 그림에서 투사층의 크기는 M = 5이므로 CBOW를 수행하고나서 얻는 각 단어의 임베딩 벡터의 차원은 5가 될 것이다.
두번째는 입력층과 투사층 사이의 가중치 W는 V x M 행렬이며, 투사층에서 출력층 사이의 가중치 W’ 는 M x V 행렬이라는 점이다. 여기서 V는 단어 집합의 크기를 의미한다.
CBOW 모델의 입력층은 원-핫 벡터로 표현되므로 그 크기는 전체 단어 사전의 크기(V)와 같다.
투사층은 학습을 통해 얻고자 하는 임베딩 벡터의 차원(M)을 의미한다고 보면 된다.
V( Vocabulary Size): 단어 사전의 크기로, 원-핫 벡터의 차원을 의미한다.
M(Embedding Dimension): 임베딩 벡터의 차원으로, 하이퍼 파라미터로 우리가 직접 설정하는 값이다.
입력층의 원-핫 벡터는 1 x V의 차원을 가진다. 이 벡터가 가중치 행렬 W와 곱해져 1 x M 차원의 추사층 벡터가 되기 위해선느, 행렬 W의 크기는 V x M이 되어야 한다.
(1×V)×(V×M)=(1×M)
따라서 W는 V x M 행렬이 맞다. 이 V x M 행렬의 각 행(row)이 바로 단어 사전의 각 단어에 해당하는 밀집 벡터(Dense Vector), 즉 우리가 최종적으로 얻고자 하는 워드 임베딩이다.
CBOW 모델은 투사층(Projection Layer)의 M 차원 벡터를 다시 출력층의 V차원 벡터(전체 단어에 대한 확률 분표)로 변환해야 한다. 이 변환을 담당하는 가중치 행렬이 W’이다.
투사층 벡터의 차원: 1 x M
W’ 의 차원 : M x V
출력층 벡터의 차원 : 1 x V
(1×M)×(M×V)=(1×V)
이 곱셈 관계를 통해 W’의 차원이 M x V여야 함을 알 수 있다.
참고로, 학습 과정에서는 W와 W’를 모두 업데이트하며, 학습이 완료된 후에는 일반적으로 W의 행 벡터를 최종적인 워드 임베딩으로 사용한다.
하지만 W’의 열(Column) 벡터도 단어 임베딩의 역할을 할 수 있다.
- W(입력 임베딩 행렬): 이 행렬은 각 행은 입력으로 들어온 단어의 입력 층(input-side) 임베딩 벡터를 나타낸다. 모델은 이 벡터들을 조합하여 문맥의 의미를 표현하는 투사층 벡터를 만든다.
- W'(출력 임베딩 행렬): 이 행렬의 각 열은 출력으로 예측해야 할 단어의 출력 측(output-side) 임베딩 벡터를 나타낸다. 투사층 벡터와 이 행렬의 곱셈을 통해 각 단어에 대한 예측 점수가 계산된다.
학습 과정은 결국 입력 측 임베딩(W)과 출력층 임베딩(W’)이 서로 잘 연결되어 문맥에 맞는 단어를 성공적으로 예측하도록 만드는 과정이다.
예를 들어 “고양이는 털이 많다.”라는 문장이 있을 때, “고양이”와 “털”이라는 단어는 함께 자주 등장하므로 모델은 이 두 단어의 임베딩 벡터가 유사한 위치에 놓이도록 학습한다.
W 행렬: “고양이” 와 “털”의 행 벡터들이 가깝게 학습된다.
W’행렬: ” 고양이”와 “털”의 열 벡터들도 가깝게 학습된다.
따라서, W’의 열 벡터들 역시 W의 행 벡터들처럼 단어 간의 유사성과 의미 관계를 담고 있는 유효한 임베딩 벡터가 된다. 다만, 일반적으로 W 행렬이 직관적인 입력 임베딩 역할을 하기 때문에 주로 이 행렬의 벡터를 최종적인 워드 임베딩으로 사용한다. 때로는 두 행렬을 모두 사용하거나 평균을 내어 성능을 높이는 연구도 진행된다.
즉, 위의 그림처럼 원-핫 벡터의 차원이 7이고, M은 5라면 가중치 W는 7 x 5행렬이고, W’ 는 5 x 7 행렬이 될 것이다.
주의 할 점은 이 두 행렬은 동일한 행렬을 전치(transpose)한 것이 아니라, 서로 다른 행렬이라는 점이다.
인공 신경망의 훈련 전에 이 가중치 행렬 W와 W’는 랜덤 값을 가지게 된다. CBOW는 주변 단어로 중심 단어를 더 정확히 맞추기 위해 계속해서 이 W와 W’를 학습해가는 구조이다.
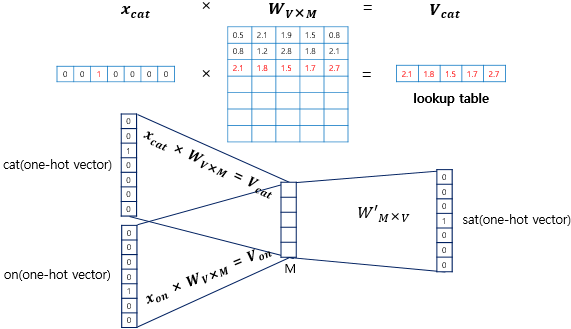
입력으로 들어오는 주변 단어의 원-핫 벡터와 가중치 W행렬의 곱이 어떻게 이루어지는가?
위 그림에서 각 주변 단어의 원-핫 벡터 x를 표기하였다.
입력 벡터는 원-핫 벡터이다. i 번째 인덱스에 1이라는 값을 가지고 그 외의 0의 값을 가지는 입력 벡터와
가중치 W 행렬의 곱은 사실 W행렬의 i번째 행을 그대로 읽어오는 것(look up)과 동일하다. 이 작업을 룩업 테이블이라고 한다. 앞서 CBOW의 목적은 W와 W’를 잘 훈련 시키는 것이라고 언급한 적 있는데 , 그 이유가 여기서 lookup해온 W의 각 행벡터가 Word2Vec 학습 후에는 각 단어의 M차원의 임베딩 벡터로 간주되기 때문이다.
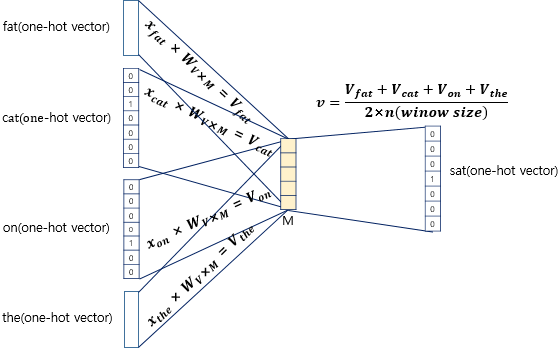
이렇게 되면 주변 단어의 원-핫 벡터에 대해서 가중치 W가 곱해서 생겨진 결과 벡터들은 투사층에서 만나 이 벡터들의 평균인 벡터를 구하게 된다.
투사층에서 벡터의 평균을 구하는 부분은 CBOW가 Skip-Gram과 다른 차이점이기도 하다.
Skip-Gram은 입력이 중심 단어 하나이기 때문에 투사층에서 벡터의 평균을 구하지 않는다.
이렇게 구해진 평균 벡터는 두번째 가중치 행렬 W’와 곱해진다.
곱셈의 결과로 원-핫 벡터들과 차원이 V로 동일한 벡터가 나온게 된다.
만약 입력 벡터의 차원이 7차원 이었다면, 여기서 나오는 벡터도 마찬가지이다.
이 벡터에 CBOW는 소프트맥스(softmax)함수를 지나면서 벡터의 각 원소들의 값은 0과 1사이의 실수로, 총 합은 1이 된다. 다중 클래스 분류 문제를 위한 일종의 스코어 벡터가 되고, 스코어 벡터의 j번째 인덱스가 가진 0과 1 사이의 값은 j번째 단어가 중심 단어일 확률을 나타낸다.
그리고 이 스코어 벡터의 값은 레이블에 해당되는 벡터인 중심 단어 원-핫 벡터의 값에 가까워져야 한다.
그리고 크로스 엔트로피로 손실함수를 사용하고 역전파 알고리즘을 써서 학습을 진행한다.
Skip-Gram
CBOW에서는 주변 단어를 통해 중심 단어를 예측했다면, Skip-gram은 중심 단어에서 주변 단어를 예측하는 것이라고 했다.
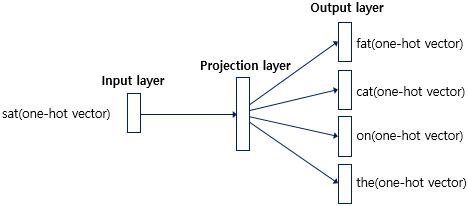
다음에 계속…
